This article by Jeffrey Bennett reprinted from Mercury magazine, Nov/Dec 1999 issue.
…scientists should be no more willing to fly blind in their teaching than they are in scientific research, where no new investigation is begun without an extensive examination of what is already known. –Bruce Alberts, former President of the National Academy of Sciences
All Mercury readers are astronomy teachers in at least some sense. Some are professional teachers at elementary, secondary, or collegiate levels. Others are research scientists whose teaching takes the form of talks and articles for the general public. And all of us spend time teaching informally when we talk to friends and family about our love of astronomy. Thus, we have all experienced the joy of seeing a face light up when a new concept becomes clear, and the frustration of having our explanations greeted by looks of bewilderment, or worse, disinterest. The purpose of this article is to help readers experience a bit more of the joy and a bit less of the frustration.
The strategies I will discuss here are intended to apply to all types of astronomy teaching, from informal discussions to complete courses. They represent a synthesis of what I have learned in 25 years of teaching and collaborating with other educators. All of them are supported by educational research, but I will try to present them in a way that appeals to readers’ intuitive ideas about teaching and learning. Those who want to go deeper should delve into the rapidly growing body of literature from the field of physics and astronomy education.
Two “Laws” of Teaching
Before moving into more specific strategies, I’ll begin with what I call the “two laws of teaching.” I have found that these two ideas work equally well with almost any audience, whether you are talking to the students in your class, to your children at the dinner table, or to your colleagues at professional conferences. Please keep in mind that these two laws must always go hand-in-hand; one of the most common mistakes in teaching occurs when someone tries to implement one law without the other.
First Law: Assume that your audience knows LESS than you think they should. In other words, don’t assume that they know facts that you think should be “obvious.” Implementing this law means reviewing basic facts before moving on to new material. Such a review will help students with weak knowledge and won’t hurt those who know the facts already (such students may even feel “smart” because they already know some of what you are saying).
Second Law: Assume that your audience is MORE intelligent than you think they are. This law goes hand-in-hand with the first because implementing it prevents you from talking down to your audience. In essence, this law is just a reminder that lack of knowledge is not the same thing as lack of intelligence. Your audience may know little about astronomy, but may still be extremely intelligent and very knowledgeable in other subject areas. A corollary to this law is that you should not “simplify” important concepts in the sense of making them simple-minded, but rather extract the key points. Indeed, much of the challenge of tailoring a presentation to an audience lies in distinguishing the key points from “details” that will only confuse your key points.
As an example of the implementation of these two laws, imagine that you are giving a public talk about recent discoveries of planets around other stars. The first law tells you not to assume that your audience knows even such basic facts as that the Sun is a star, or the difference between stars, planets, and moons. (A small but significant fraction of my college students do not know that the Sun is a star when they enter my classes.) It takes only a couple of minutes to remind the audience of these facts, but without them the rest of your talk will be meaningless. The second law tells you that even if your audience knows little about astronomy, you can still feel free to talk about fairly subtle concepts as long as they are “key” concepts and you build up to them appropriately. For example, in a talk about planets around other stars, you can discuss subtle detection techniques, even if your audience didn’t know that the Sun was a star when the talk began. (Here’s a 15-minute outline: explain the Doppler effect for light by relating it to the more familiar Doppler effect for sound; point out that while we usually think of planets orbiting stars, objects actually orbit mutually around a common center of mass; use this idea to explain how an observer in another star system could notice Jupiter’s effect on the Sun; and then put all of it together to explain how Doppler measurements allow us to detect subtle stellar motions that we can attribute to the influence of an orbiting planet.) The second law also tells you to pay attention to audience reactions: If you are greeted by perplexed looks, assume it is because of an inadequacy in your explanation, and keep refining it or trying alternative explanations until you find a way to make your point clear.
Five Key Strategies For Astronomy
With the two laws as background, I’ll now present five key strategies that are useful to teaching astronomy to non-specialists. In each case, I will discuss the premises behind the strategy (i.e., why they work) and suggest methods for implementation. While these strategies apply to all types of teaching, I will discuss them primarily in the context of teaching a course in astronomy at the high school or college level.
Strategy 1: Provide A Contextual Framework
As put eloquently in Poincare’s quotation at the beginning of this article, science is much more than just a collection of facts. Just as a builder cannot know where to place bricks without having some idea of the structure of a house, we cannot expect students to absorb scientific facts without having a context in which to place them. Thus, the first key strategy for teaching astronomy is to provide your students with a mental edifice, often called a contextual framework, within which they can organize the astronomical concepts and facts that you want them to learn.
We can see the importance of a contextual framework with a simple example. You’ve probably noticed that many students confuse the terms solar system and galaxy -sometimes using them interchangeably even after completing a course in astronomy (in someone else’s class!). Astronomers are often shocked to find people confusing such different concepts, but it is really not so surprising. After all, pictures of planets and galaxies are about the same size when printed in a book or projected on a screen, so how is a student to know that they actually differ in size by more than a dozen orders of magnitude? Without a contextual framework within which to compare and relate these objects, students have no place to mentally “file” any facts associated with them. Moreover, note that this problem is particularly insidious because it can be so easily hidden from instructors. Continuing our example, a student may be able to regurgitate plenty of isolated facts about a solar system or galaxy, thereby proceeding through an entire course and achieving a good grade, even while having missed the most basic ideas about how these objects differ.
Which one is bigger? On the page, the galaxy and the planet look to be about the same size. Thus, you cannot expect students to understand the vast difference in scale (a factor of about 103 in diameter!) unless you first provide them with a contextual framework that helps them understand the hierarchy of structure in the Universe. Images courtesy of AURA/STScI and NASA.
Providing an appropriate contextual framework is particularly important in astronomy because so few students have any such framework from prior learning. In fact, following the first law of teaching above, you should assume that your audience lacks the necessary contextual framework. The elements of a framework that you will need to provide depend, of course, on the material you plan to discuss. For a general or informal talk, you will have time only to introduce the framework directly relevant to your topic. For an introductory course in astronomy, I believe that the contextual framework should consist of the following four “big picture” elements:
The basic hierarchy of structure in the Universe.
For example, make sure that students understand the elements and the relationships among the elements of our “cosmic address” (i.e., Earth, Solar System, Milky Way Galaxy, Local Group, Local Supercluster, Universe).
A basic overview of modern astronomical ideas concerning our cosmic origins.
This is an appropriate place to mention that the Universe is expanding in the sense that galaxies are moving farther apart on average, which implies that everything was close together at some time in the past. By doing this, you can immediately demystify the term Big Bang, which nearly all students have heard but which evokes in their minds the erroneous image of some mysterious explosion.
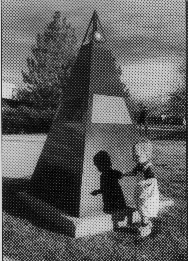A model Solar System is a very useful device for providing a contextual framework on astronomical scales. Here we see the model Sun (on top of the pyramid) at one-ten billionth actual size in the Colorado Scale Model Solar System. The model planets are housed in smaller granite pedestals along a walkway extending to the left. At this scale, the Earth is located 15 meters away and is the size of a pinhead; Jupiter is located 78 meters away and is the size of a marble; and Pluto lies at a mean distance of 590 meters, and is about the size of the period at the end of this sentence. The child is the author’s son, getting his first lesson about the scale of the Universe. Photo courtesy of author.
A general sense of the scale of space and time.
Note that it is very important to present ideas of scale in a way that gives students some perspective, as opposed to a way that merely tells them numerical relationships. For example, the popular “powers of 10” approach to scale works well only for those students who understand orders of magnitude, and fails for the many students with weak mathematical skills. In contrast, an approach that compares astronomical scales to familiar scales works effectively for everyone. I like to use a scale model of the Solar System as the starting point for the scale of space. For time, I like to use Carl Sagan’s device of the cosmic calendar, in which we imagine the history of the Universe from the Big Bang to the present compressed into a single year.
The number of stars in the observable Universe is of order 1022. One way to give meaning to this number – and thereby help students develop a contextual framework for the enormity of the Universe is to have students imagine counting grains of sand on the beach. The number of stars in the observable Universe is greater than the total number of grains of sand on all the beaches everywhere on Earth (counting only beach sand, not sand on the ocean floor). Photo courtesy of M. Voit.
A general sense of the dynamics of the Universe.
As example, Earth rotates on its axis, revolves around the Sun, orbits the Galactic Center, and moves relative to distant galaxies because of universal expansion. Note that you can use this discussion of motion to explain basic sky phenomena, such as daily motions of stars and the cause of the seasons. This is also an excellent opportunity to demystify how the motions of distant galaxies lead to the idea of an expanding Universe with a raisin cake analogy.
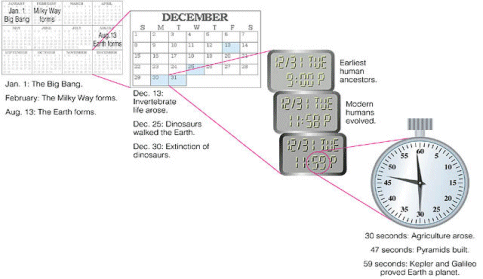
One way to illustrate the scale of time is with a cosmic calendar…
Demystifying the Idea of an Expanding Universe…
Third, note that while the importance of a contextual framework is clearly supported by educational research, it is completely neglected by one traditional approach to teaching astronomy. This approach tries to teach students astronomy in the same way that astronomy developed historically, beginning by telling students only what the ancient Greeks knew and then working through the Copernican revolution and onward to modern astronomy. While this approach can succeed for students who are capable of gradually cobbling together their own contextual framework (and already have such a framework from prior study), most students fare much better if the framework is built explicitly. (The traditional approach also suffers in another way: Many discarded ancient beliefs are rooted in observations that feed common misconceptions; if these beliefs are discussed before the misconceptions have been addressed, they may actually reinforce the misconceptions rather than help students understand how astronomy has progressed.)
Strategy 2: Create Conditions For Conceptual Change
Most teachers recognize that a student cannot learn a new concept without making a personal effort, which is why simple lecturing is a fairly ineffective form of teaching (see, for examples, “Restructuring a Class, Transforming the Professor,” Jul/Aug 1998, p. 16; “What to Do in a Big Lecture Class, Besides Lecture?” Jan/Feb 1999, p. 14; and “The Play1s the ThingS Some Thoughts on Introductory Physics Teaching,” Sep/Oct 1999, p. 24). Less recognized, however, is that teaching also involves the unlearning of mistaken ideas that can get in the way of real understanding. For example, most students have “learned” that there is no gravity in space. Unless you first help them unlearn this idea, they cannot truly understand Newton1s law of gravity. In other words, true learning involves what educational researchers call conceptual change, in which a student replaces an erroneous idea about some concept with a correct idea.
Conceptual change rarely occurs when students are simply given a body of facts to digest. Instead, it occurs when you help students both to recognize the inadequacy of their current understanding and to build a better understanding in its place. Thus, the second key strategy is to create conditions in which conceptual change is more likely to occur, which you can do with two simple techniques:
Always build bridges between new concepts and familiar ones.
These “bridges to the familiar” help students see how new concepts connect to older ones, and also allow them to check the internal consistency of their personal understanding.
Why are astronauts weightless in space? If your students say it is because there is no gravity in space, follow-up by asking them why the Moon orbits Earth. Most will know that it does so because of gravity, and will, therefore, realize that their original answer about the astronauts cannot be correct. This “personal paradox” makes the students more receptive to learning the correct reason why astronauts are weightless in space. Photo courtesy of NASA.
Whenever possible, confront students with “personal paradoxes” that force them to face problems in their preconceived notions about some concept.
As an example, let’s apply these techniques to the “no gravity” misconception. Instead of simply telling the students that they are wrong, try this approach: First ask your students why astronauts are weightless in Earth orbit. Most will answer that it is because there is no gravity in space. Next ask them why the Moon orbits Earth. Most are aware that the Moon orbits Earth because of gravity and will tell you so – and you will literally see their jaws drop as they recognize the inconsistency in their two answers. Thus, you have used bridges to familiar ideas (astronauts, the Moon) to create a “personal paradox” in which students realize that their own ideas about gravity are inconsistent, and they therefore become receptive to learning new ideas.
For a more complex example, consider teaching about surface features on the planets. If you present these features as a collection of facts, they will be forgotten soon after an exam. But if you discuss them in the context of geology, and relate them to familiar geological structures on Earth, you can create conceptual change in how students think about geology. In that way, you can help your students understand geological features both on Earth and other planets. I’ve heard some instructors argue that this is more difficult for students than just memorizing the facts, but this argument misses the point. Memorization is easier if you’re thinking only in terms of tomorrow1s exam, but if you actually want your students to learn something, it must occur through conceptual change.
Strategy 3: Make the Material Relevant
In an ideal world, students would learn simply because of inherent curiosity. In reality, most students are far more motivated to learn when they can see the relevance of the subject matter to their own lives. In this respect, we are fortunate in astronomy: The desire to understand our connections to the cosmos is a unifying human trait across all cultures, and most students therefore come to our classes with an intuitive sense that astronomy is relevant to their lives. Thus, the third key strategy is to be explicit about the connections between astronomy and questions about human existence, at least to the extent possible. Here are several examples:
- When presenting basic ides from physics, put them into a context that is meaningful in everyday life. For example, introduce ideas about light emission, absorption, and reflection by discussing why a red shirt is red in daylight, unseen in darkness, and yellowish under low-pressure sodium lights.
- When discussing our solar system, emphasize how learning about other planets helps us understand Earth.
- When covering stellar evolution, focus on the idea that we are “star stuff” (in the words of Carl Sagan).
- When covering galaxies, focus on galactic evolution and how it has helped create the conditions that make our existence possible.
Strategy 4: Limit Use of Jargon
I once heard that the number of new terms introduced in a typical astronomy course is larger than the number of words taught in the first semester of a foreign language course. While I’m not sure if this is literally true, it makes an important point: We can hardly expect students to learn a new subject if we are teaching it to them in a foreign language. Thus, it is absolutely imperative that we limit the use of jargon in teaching.
A typical, jargon-laden caption for this photo might read, “This footprint was created when an astronaut’s weight compacted the lunar regolith to leave a boot-bottom impression.” But the idea is much clearer without the jargon: “Astronauts left footprints in the powdery soil (or dust) that covers the lunar surface.” Photo courtesy of NASA.
Use the vernacular when discussing planetary features. For example, you can safely refer to Mercury’s scarps as “cliffs,” and to the lunar regolith as “powdery lunar soil.” (If you are concerned that “soil” implies organic matter, you can use the term “dust” instead.)
For most purposes in introductory astronomy, the important distinction among supernovae is that between massive stars that explode at the ends of their lives and white dwarfs that explode when they exceed the Chandrasekhar limit. So why not just refer to them as “massive star supernovae” and “white dwarf supernovae,” rather than as Type II and Type Ia? (And refer to the Chandrasekhar limit as the “white dwarf limit.”)
When a star or cloud of gas is contracting because gravity is stronger than its internal pressure, we say that it is undergoing “gravitational contraction.” This is a good term, because it describes what is actually happening. But when pressure balances gravity, we say that the object is in a state of hydrostatic equilibrium – even though this equilibrium has little to do with either hydrogen or water. Simply replacing this term with “gravitational equilibrium” makes it much easier for students to understand what you are talking about. (Thanks here to Mitch Begelman and Martin Rees, who introduced the term gravitational equilibrium in their book Black Holes: Gravity’s Fatal Attraction [Scientific American Books, 1996].)
On a closely related note, be careful about your use of diagrams and graphs. Supposedly “popular” talks are often sprinkled with complex graphics that are almost impossible for the non-specialist to interpret. Consider the Hertzsprung-Russell diagram: the axes are so unusual and counterintuitive that it takes the average person at least a few hours of study to understand this diagram. While this is fine in a semester-long course, it makes the diagram fairly useless in an hour talk.
Strategy 5: Challenge Your Students
The final key strategy harks back to the second law of teaching above: Don’t be afraid to challenge your students. Students can learn surprisingly difficult material when they have a special interest in learning it. And, because many students are intensely curious about many topics related to astronomy, you can teach them many challenging concepts. For example:
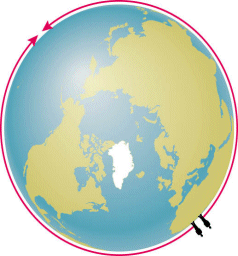
Students are curious about relativity and therefore willing to work hard to learn it. This diagram shows a simple analogy that helps them understand the role of geometry in relativity by considering the role of geometry on Earth. Two people setting off in opposite directions on the planet will eventually meet, even though they never deviate from the straightest possible paths. We attribute this meeting to the fact that Earth is round. In a similar way, two spaceships launched in opposite directions with the same orbital speed will also meet as they orbit Earth. Doesn’t it therefore seem more natural to attribute this meeting to something about the geometry of the Universe than to a mysterious force called gravity, which acts at distance for no apparent reason? Figure reprinted with permission from The Cosmic Perspective, by Bennett, Donahue, Schneider, and Voit (Addison Wesley, 1999).
Similarly, most students have heard of the Heisenberg uncertainty principle and are curious about it. Thus, you can take advantage of this curiosity to give a qualitative introduction to key quantum ideas (e.g., uncertainty and exclusion) that are relevant to astronomical topics such as degeneracy pressure, inflation in the early Universe, and black hole evaporation.
I don’t think I’ve ever met a student who didn’t want to know about black holes. If you’ve covered a few ideas of relativity and quantum mechanics, you can give your students a real understanding of black holes, and they will be fascinated despite the challenging nature of the concepts.
Putting It All Together
I hope that the strategies discussed here will be useful to readers in future teaching efforts, but remember that there is no foolproof recipe for teaching success. Every teacher has a unique style of presentation, and every student has a unique style of learning. Good teaching therefore means adapting to your students1 needs, and always being willing to try a new strategy when an old one fails. It1s hard work, and requires constant effort to improve. But modern astronomy is a subject that belongs to the public at large: the public pays for it, supports it, wants to know about it. We owe it to society to make whatever effort is required.